poznamky vestibularni system - nečíst
Moderátor: Lucid Dreaming Project
poznamky vestibularni system - nečíst
Zkratky:
F - fyzická
N - nefyzická
Smysly
P - Propriorecepce
V - Zrak
A - Sluch
T - hmat + tepltota (Term)
Ac - akcelerace
B - vestibular (G+Ac)
G - gravitace
S -čich
Ch -chut
R - Zdroje
P - Priorita
D - Data
F - fyzická
N - nefyzická
Smysly
P - Propriorecepce
V - Zrak
A - Sluch
T - hmat + tepltota (Term)
Ac - akcelerace
B - vestibular (G+Ac)
G - gravitace
S -čich
Ch -chut
R - Zdroje
P - Priorita
D - Data
Help! I'm a multidimensional being trapped in a linear time-space continuum!
Re: poznamky 2 - nečíst
podle místa V > T > A
podle času A > T> V
A x > A z
ruka P y > P x
F pozornost(focus)
podle času A > T> V
A x > A z
ruka P y > P x
F pozornost(focus)
Help! I'm a multidimensional being trapped in a linear time-space continuum!
Vestibular
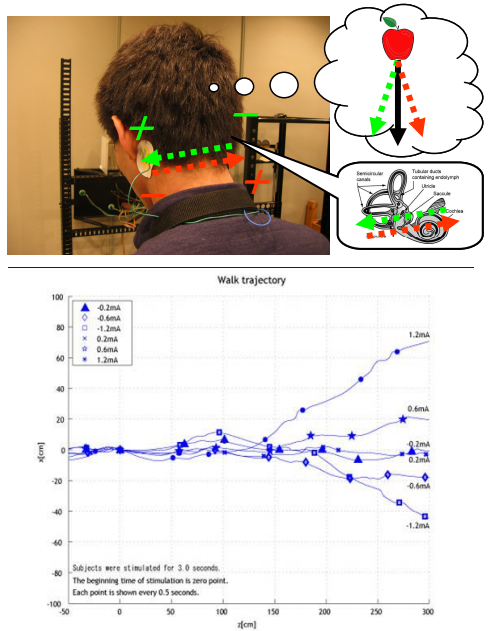



Without this signal, there are no messengers telling the brain, or the body, where it is in space. There is a complete disconnection between the body and its ability to perceive what is up, down or sideways, much like zero gravity in outer space.
*Hold your index finger a few inches in front of your face and sweep it back and forth at a rate of maybe once or twice a second. What do you see? A blurry finger. Now hold your finger steady and instead shake your head back and forth at the same half-second pace. This time, no blur, no Marcel Duchamp’s “Nude Descending a Staircase” effect. The finger stays in focus even as your head vigorously pantomimes its denial.








Help! I'm a multidimensional being trapped in a linear time-space continuum!
ves
The Cause of Spatial Disorientation
http://ftp.rta.nato.int/public//PubFull ... 086-01.pdf
If, for example, we are rotated on and about an earth vertical axis with a constant velocity, our sense of
(angular) motion will vanish within tens of seconds (Fig. 2)
Inertia and gravity
If we are moved in space, there are only six degrees of freedom (DoF) to be dealt with. We can be translated,
giving rise to a change in position or velocity, and this may be characterised by the linear acceleration
a=d2x/dt2, a vector with three components along three (orthogonal) axes. A rotation may additionally change
the orientation, and this can be characterised by a three component angular velocity vector ω. Within each of
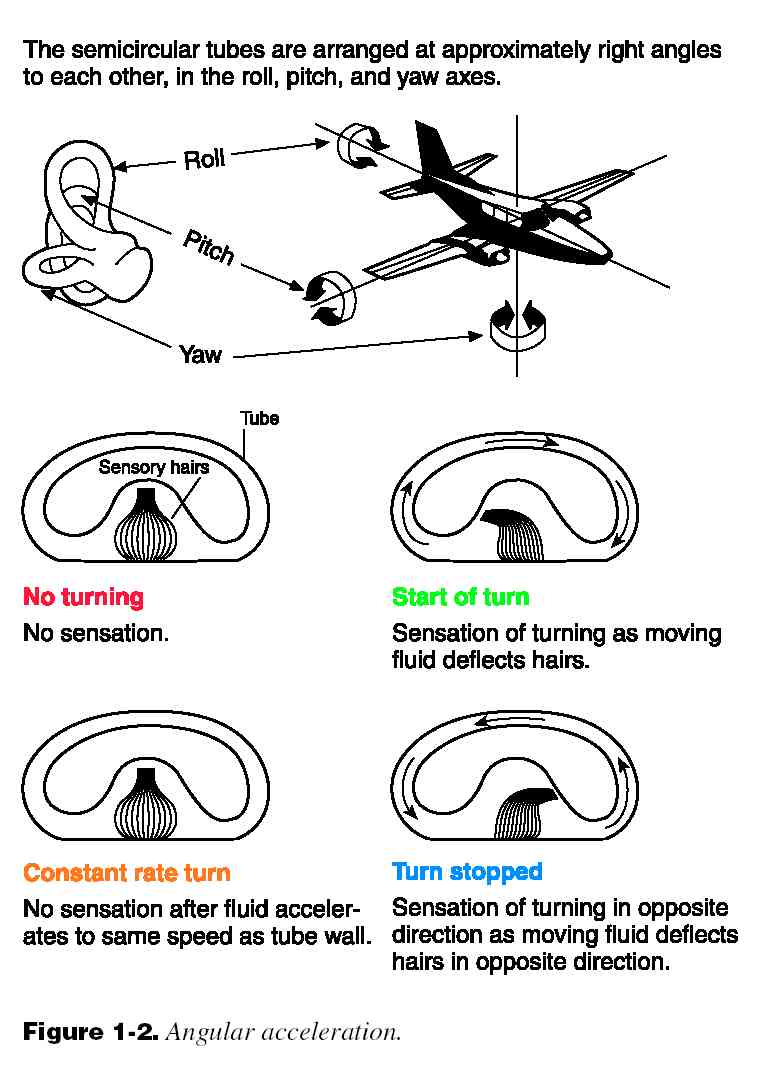
our inner ears there are three more or less orthogonal semicircular canals (SCC), filled with fluid
(endolymphe), which fluid will lag the head due to inertia. A piston-like valve (culupa) detects this flow of
fluid, and signals the head rotation. Due to friction and the fact that the cupulae are fixed to the head, the
fluid flow is damped, such that the neural canal
signals are proportional to a high pass filtered angular
velocity signal (e.g. van Egmond et al., 1949; Robinson, 1977). This implies that the SCC are insensitive to
constant angular head velocity, and this is just what causes the illusions shown in Figs. 2 and 3
Within the sac connecting the canals, there are two layers
of heir cells with crystals on top (the otoliths, see
Fig. 8, which crystals have a higher specific density than the surrounding matter, such that these will lag due
to inertia too, here to linear motion (
a=d2x/dt2
). However, these otoliths will also be attracted by gravity on
earth (see Fg. 9, and they will also signal proportional to gravity (
g=Fg/m
). Therefore, also these otolithic
sensors are not capable of discerning inertial from gravitational accelerations. This results in 9 DoF that have
to be dealt with on earth (i.e. 3 inertial acceleration components, 3 gravity components, and 3 angular
velocity components). For the remainder we assume that
the otoliths transduce the resultant acceleration, or
specific force, near perfection (e.g. Merfeld et al., 1993), i.e. their output is proportional to
f=a+g
*f=ac+g
the accelerations due to motion (inertia) en due to gravity are indistinguishable,
and if we would not discern gravity as such, we might feel like an astronaut within five minutes (
∆x=∫∫gdt2= ½gt2≈440 km, with g= 9.81 m/s2and∆t= 300 s). Obviously we do not feel this, and apparently our CNS
does do something to the otolith afferents to make the distinction. Another example includes tilt. When tilted
on earth, the gravitational acceleration may be exactly e
qual to the resultant of gravity and an acceleration
forward and slightly downward (see Fig. 10) In the first example, some CNS-processing on otolith afferents
only is requested, while in the second example, angular information from the SCC may aid in the solution to
estimate motion and gravity. How this function of the CNS may be described mathematically is summarised
in the next section on a spatial orientation model.
Circular vection: Ves + V
If we are looking at a moving environment rotating about an earth vertical axis while
sitting still, within several seconds we will experience a self rotation, instead of object rotation. This
phenomenon is called circular vection. This sense of motion can be achieved by any visual stimulus, as long
as changes in contrast are present. No interpretable structures are required, and a random dotted pattern
suffices. This means that optic flow, characterised by velocity (here angular velocity) is the determinant of
vection. If this sense of self motion is next combined with the deficient sense of self rotation during true self
motion when rotating about an earth vertical axis in the dark at constant velocity, these two signals will just
add to a veridical sense of self motion. This is illustrated in Fig. 13
Fig. 13.
Circular vection. When rotated about an earth
vertical axis, visual motion will result in a
slowly increasing sense of self motion, while tr
ue body motion will result in a slowly decreasing
sense of self motion. The addition of both
results in a true sense of self motion
Linear vection:
Something similar holds for linear vection, and this is most often exemplified by the train
that is leaving the platform next to ours, inducing a strong sense of self motion in the opposite direction.
Because this process is not counteracted by filtering of motion sensor signals as is the case with angular
motion, linear vection is much faster than circul
ar vection. Because we do not “see” acceleration, linear
vection should be characterised in terms of velocity, and linear motion as sensed by the vestibular system
(i.e. linear acceleration) should accordingly be integrat
ed over time before it can interact with the visual
velocity perception. At first order approximation we assume a linear weighted addition (c.f. Howard, 1997)
of vestibular and visual velocity signals to take pl
ace to determine the final linear velocity perception. Vision
will generally be dominant in this process (e.g. the train illusion).
Attitude perception:
Things get more complicated when describing the visual-vestibular interactions with
respect to attitude perception. Then, there are (at least) three factors of interest. First vestibular cues are at
steak, as described in the previous section. Second, visual cues can be separated in polarity and frame
information. Trees and houses generally point upward, while horizontal and vertical structures aid in
determining horizontality and verticality. Lastly, there is also a sense of verticality determined by our own
longitudinal body axis. This effect is most evident in weightlessness, when subjects can still indicate their
sense of verticality, which, generally aligns with their longitudinal body axis. This contribution is called the
idiotropic vector (Mittelstaedt, 1983). These contributions
are sketched in Fig. 14, and they are also assumed
to interact by means of a linear weighted addition
A visual-vestibular spatial orientation model
Putting these assumptions together, we come up with a model as sketched in Fig 15. According to this
model, spatial orientation is thus characterised by at least four variables, in this case four vectors, with three
(Cartesian) components each. These variables are linear
acceleration, linear velocity, angular velocity, and
our sense of attitude means of the estimate of the gravitational vector. Because linear acceleration is closely
linked to force by Newton’s second law (
F=ma), the perception of acceleration may also be closely related
to force perception. The estimation of the gravitational v
ector is also called the subjective vertical (SV). Due
to the different interactions involved, the four variable
s may all behave differently, and are therefore (partly)
independent. When characterising spatial orientation this way (i.e. by means of four vectors), it will also be
evident that spatial orientation is a complex matter, which interpretation is further complicated by our limited
intuitive sense to form a notion of (mainly angular) motions and attitude in three-dimensional space
*gular velocity is always below 3°/s,which is assumed to be below the threshold for angular motion perception.
n the simple servo model of Fig. 1, sensory
deficiencies and CNS delays will directly deteri
orate the system’s performance. To overcome these
problems, it is nowadays believed that the central ner
vous system uses a so called internal model of the body
dynamics, that, when fed with a copy of the motor commands (the efference copy), may give a prediction of
body motion that is more accurate than that estimated by our sensory system (Bos & Bles, 2002). If this
internal model next includes a copy of the sensory dynami
cs as well, the difference between true sensory and
internal model afferents may be used in addition for adaptation purposes. Optimally this difference should, of
course, be zero. We have previously shown that this difference, or conflict, when modelled properly,
correlates well with motion sickness (Bos & Bles, 1998, 2002; Bles et al., 2000). Another extension concerns
the addition of somatosensory cues, also referred to as
“the seat of the pants”. If, for example, acceleration
perception is linked with force perception as stated earlier, than we will need the interaction with
somatosensory cues to command the oscillating perception of acceleration after the centrifuge deceleration in
n the simple servo model of Fig. 1, sensory
deficiencies and CNS delays will directly deteri
orate the system’s performance. To overcome these
problems, it is nowadays believed that the central ner
vous system uses a so called internal model of the body
dynamics, that, when fed with a copy of the motor commands (the efference copy), may give a prediction of
body motion that is more accurate than that estimated by our sensory system (Bos & Bles, 2002). If this
internal model next includes a copy of the sensory dynami
cs as well, the difference between true sensory and
internal model afferents may be used in addition for adaptation purposes. Optimally this difference should, of
course, be zero. We have previously shown that this difference, or conflict, when modelled properly,
correlates well with motion sickness (Bos & Bles, 1998, 2002; Bles et al., 2000). Another extension concerns
the addition of somatosensory cues, also referred to as
“the seat of the pants”. If, for example, acceleration
perception is linked with force perception as stated earlier, than we will need the interaction with
somatosensory cues to command the oscillating perception of acceleration after the centrifuge deceleration in
Fig. 19.
http://ftp.rta.nato.int/public//PubFull ... 086-01.pdf
If, for example, we are rotated on and about an earth vertical axis with a constant velocity, our sense of
(angular) motion will vanish within tens of seconds (Fig. 2)
Inertia and gravity
If we are moved in space, there are only six degrees of freedom (DoF) to be dealt with. We can be translated,
giving rise to a change in position or velocity, and this may be characterised by the linear acceleration
a=d2x/dt2, a vector with three components along three (orthogonal) axes. A rotation may additionally change
the orientation, and this can be characterised by a three component angular velocity vector ω. Within each of
our inner ears there are three more or less orthogonal semicircular canals (SCC), filled with fluid
(endolymphe), which fluid will lag the head due to inertia. A piston-like valve (culupa) detects this flow of
fluid, and signals the head rotation. Due to friction and the fact that the cupulae are fixed to the head, the
fluid flow is damped, such that the neural canal
signals are proportional to a high pass filtered angular
velocity signal (e.g. van Egmond et al., 1949; Robinson, 1977). This implies that the SCC are insensitive to
constant angular head velocity, and this is just what causes the illusions shown in Figs. 2 and 3
Within the sac connecting the canals, there are two layers
of heir cells with crystals on top (the otoliths, see
Fig. 8, which crystals have a higher specific density than the surrounding matter, such that these will lag due
to inertia too, here to linear motion (
a=d2x/dt2
). However, these otoliths will also be attracted by gravity on
earth (see Fg. 9, and they will also signal proportional to gravity (
g=Fg/m
). Therefore, also these otolithic
sensors are not capable of discerning inertial from gravitational accelerations. This results in 9 DoF that have
to be dealt with on earth (i.e. 3 inertial acceleration components, 3 gravity components, and 3 angular
velocity components). For the remainder we assume that
the otoliths transduce the resultant acceleration, or
specific force, near perfection (e.g. Merfeld et al., 1993), i.e. their output is proportional to
f=a+g
*f=ac+g
the accelerations due to motion (inertia) en due to gravity are indistinguishable,
and if we would not discern gravity as such, we might feel like an astronaut within five minutes (
∆x=∫∫gdt2= ½gt2≈440 km, with g= 9.81 m/s2and∆t= 300 s). Obviously we do not feel this, and apparently our CNS
does do something to the otolith afferents to make the distinction. Another example includes tilt. When tilted
on earth, the gravitational acceleration may be exactly e
qual to the resultant of gravity and an acceleration
forward and slightly downward (see Fig. 10) In the first example, some CNS-processing on otolith afferents
only is requested, while in the second example, angular information from the SCC may aid in the solution to
estimate motion and gravity. How this function of the CNS may be described mathematically is summarised
in the next section on a spatial orientation model.
Circular vection: Ves + V
If we are looking at a moving environment rotating about an earth vertical axis while
sitting still, within several seconds we will experience a self rotation, instead of object rotation. This
phenomenon is called circular vection. This sense of motion can be achieved by any visual stimulus, as long
as changes in contrast are present. No interpretable structures are required, and a random dotted pattern
suffices. This means that optic flow, characterised by velocity (here angular velocity) is the determinant of
vection. If this sense of self motion is next combined with the deficient sense of self rotation during true self
motion when rotating about an earth vertical axis in the dark at constant velocity, these two signals will just
add to a veridical sense of self motion. This is illustrated in Fig. 13
Fig. 13.
Circular vection. When rotated about an earth
vertical axis, visual motion will result in a
slowly increasing sense of self motion, while tr
ue body motion will result in a slowly decreasing
sense of self motion. The addition of both
results in a true sense of self motion
Linear vection:
Something similar holds for linear vection, and this is most often exemplified by the train
that is leaving the platform next to ours, inducing a strong sense of self motion in the opposite direction.
Because this process is not counteracted by filtering of motion sensor signals as is the case with angular
motion, linear vection is much faster than circul
ar vection. Because we do not “see” acceleration, linear
vection should be characterised in terms of velocity, and linear motion as sensed by the vestibular system
(i.e. linear acceleration) should accordingly be integrat
ed over time before it can interact with the visual
velocity perception. At first order approximation we assume a linear weighted addition (c.f. Howard, 1997)
of vestibular and visual velocity signals to take pl
ace to determine the final linear velocity perception. Vision
will generally be dominant in this process (e.g. the train illusion).
Attitude perception:
Things get more complicated when describing the visual-vestibular interactions with
respect to attitude perception. Then, there are (at least) three factors of interest. First vestibular cues are at
steak, as described in the previous section. Second, visual cues can be separated in polarity and frame
information. Trees and houses generally point upward, while horizontal and vertical structures aid in
determining horizontality and verticality. Lastly, there is also a sense of verticality determined by our own
longitudinal body axis. This effect is most evident in weightlessness, when subjects can still indicate their
sense of verticality, which, generally aligns with their longitudinal body axis. This contribution is called the
idiotropic vector (Mittelstaedt, 1983). These contributions
are sketched in Fig. 14, and they are also assumed
to interact by means of a linear weighted addition
A visual-vestibular spatial orientation model
Putting these assumptions together, we come up with a model as sketched in Fig 15. According to this
model, spatial orientation is thus characterised by at least four variables, in this case four vectors, with three
(Cartesian) components each. These variables are linear
acceleration, linear velocity, angular velocity, and
our sense of attitude means of the estimate of the gravitational vector. Because linear acceleration is closely
linked to force by Newton’s second law (
F=ma), the perception of acceleration may also be closely related
to force perception. The estimation of the gravitational v
ector is also called the subjective vertical (SV). Due
to the different interactions involved, the four variable
s may all behave differently, and are therefore (partly)
independent. When characterising spatial orientation this way (i.e. by means of four vectors), it will also be
evident that spatial orientation is a complex matter, which interpretation is further complicated by our limited
intuitive sense to form a notion of (mainly angular) motions and attitude in three-dimensional space
*gular velocity is always below 3°/s,which is assumed to be below the threshold for angular motion perception.
n the simple servo model of Fig. 1, sensory
deficiencies and CNS delays will directly deteri
orate the system’s performance. To overcome these
problems, it is nowadays believed that the central ner
vous system uses a so called internal model of the body
dynamics, that, when fed with a copy of the motor commands (the efference copy), may give a prediction of
body motion that is more accurate than that estimated by our sensory system (Bos & Bles, 2002). If this
internal model next includes a copy of the sensory dynami
cs as well, the difference between true sensory and
internal model afferents may be used in addition for adaptation purposes. Optimally this difference should, of
course, be zero. We have previously shown that this difference, or conflict, when modelled properly,
correlates well with motion sickness (Bos & Bles, 1998, 2002; Bles et al., 2000). Another extension concerns
the addition of somatosensory cues, also referred to as
“the seat of the pants”. If, for example, acceleration
perception is linked with force perception as stated earlier, than we will need the interaction with
somatosensory cues to command the oscillating perception of acceleration after the centrifuge deceleration in
n the simple servo model of Fig. 1, sensory
deficiencies and CNS delays will directly deteri
orate the system’s performance. To overcome these
problems, it is nowadays believed that the central ner
vous system uses a so called internal model of the body
dynamics, that, when fed with a copy of the motor commands (the efference copy), may give a prediction of
body motion that is more accurate than that estimated by our sensory system (Bos & Bles, 2002). If this
internal model next includes a copy of the sensory dynami
cs as well, the difference between true sensory and
internal model afferents may be used in addition for adaptation purposes. Optimally this difference should, of
course, be zero. We have previously shown that this difference, or conflict, when modelled properly,
correlates well with motion sickness (Bos & Bles, 1998, 2002; Bles et al., 2000). Another extension concerns
the addition of somatosensory cues, also referred to as
“the seat of the pants”. If, for example, acceleration
perception is linked with force perception as stated earlier, than we will need the interaction with
somatosensory cues to command the oscillating perception of acceleration after the centrifuge deceleration in
Fig. 19.
Help! I'm a multidimensional being trapped in a linear time-space continuum!
Re: poznamky 2 - nečíst
First,the angular velocity sensors(semicircular canals) provide no low-frequency information, whereas specific force sensors (otoliths) do provide such information
V+Ves effect delay
The delay is undetectable when visual stimulus magnitude is near vestibular thresholds, and the delay vanishes in the presence of confirming vestibular cues of sufficient magnitude
* zvísi na integraci / boji V a Ves
http://www.mbfys.ru.nl/staff/j.vangisbe ... d_1988.pdf
Merfeld and colleagues rotate an
upright subject in the dark until the canals
completely adapt and the sensation of
rotation is abolished (
Fig. 3a
and
d
). This
happens because the canals are bony cir-
cular tubes, filled with fluid and spanned
by a flexible membrane (the cupola),
which behave somewhat like a bucket of
water. If you pick up a bucket and twist it,
the fluid at first stays still, and the bucket
turns around it. Friction of the fluid on
the moving walls of the bucket eventually
causes the fluid to ‘catch up’ to the buck-
et. In the canals, the initial lag causes the
fluid to exert force on the cupula, which
stretches in response. Hair cells register
this stretch, which modulates neuronal
firing. As the fluid catches up with the
canal, the elasticity of the cupula restores
it to its resting state, the hair cells no
longer sense stretch, and neuronal mod-
ulation ceases. This process takes about
twenty seconds, but the central ‘memory’
of the stimulus lasts longer, so the authors
wait two minutes for the rotating subject
Fig. 1.
Anatomy of the vestibular system. The
vestibuluar appartatus consists of three semi-
circular canals, which detect angular motion,
and two otolith organs (red and green), which
detect linear motion. The entire structure,
along with the cochlea, is encased within solid
bone in the inner ear.
Acceleration
Inertial
force
Gravity
Fig. 2.
Gravitational and inertial forces have
identical effects on the otolith organs.
(a)
A
hair cell from the saccule, stimulated by the
effect of gravity on the otolithic mass when
the head is tilted nose-up.
(b)
Same hair cell
stimulated by inertial force when the upright
head is accelerated forward. The hair cell
deflections in
(a)
and
(b)
are indistinguishable.
to lose all sensation of move-
ment. The subject is then
decelerated to a sudden stop,
which causes hair cells to sense
the cupula being stretched in
the opposite direction. Because
the canals and central circuits
were completely adapted to
(for example) a counter-clock-
wise rotation, this deceleration
produces exactly the same
response as an acceleration in
the opposite (clockwise) direc-
tion (
Fig. 3b
and
e
). Finally,
the subject is tilted nose-up
(
Fig. 3c
), and the eye move-
ments elicited by the vestibu-
lo-ocular reflex are used to
determine how the vestibular
system’s internal model inter-
prets this confusing input.
The vestibular system is
confronted with a paradox
(
Fig. 3f
). From the nose-up
position, the sensation of
clockwise rotation leads it to
expect the head to move so
that the right ear is down.
However, because no rotation
is actually occurring, the head
remains nose-up. The otolith
organs report that the back of
the head, not the right ear, is
‘down’. Hence the paradox: the
canals report that the head is rotating
clockwise and should therefore be turned
right ear down, while the otoliths report
a gravitational vector aligned with the
back of the head, as if no rotation has
occurred. To resolve this paradox, the
vestibular system postulates a leftward
force that would satisfy these conflicting
constraints. An illusory leftward inertial
force of the correct magnitude exactly
accounts for the difference between what
the otoliths report—that the back of the
head is pointing down—and what the
illusory rotation implies—that the right
ear is pointing down (
Fig. 3f
). Such a
force would be produced if the head were
accelerating to the right.
Subjects do not report translation, per-
haps because they are too disoriented by
the unusual sequence of stimuli to prop-
erly sort out their sensations. However,
their eyes betray them. Merfeld and col-
leagues compare evoked movements when
clockwise or counterclockwise rotation
precedes a particular head tilt. After sub-
tracting out the reflexive response to the
illusory rotation and the subsequent tilt,
a residual signal remains. This residual eye
otolith signals
9,10
. On the cur-
rent evidence, however, it is
not possible to rule out
involvement of the vestibular
nucleus.
The vestibulo-ocular sys-
tem has already provided sev-
eral less-complicated examples
of internal models. The cen-
tral ‘velocity storage’ mecha-
nism that maintains the sense
of rotation for a minute or
more after the canals have
adapted
11
is itself a simple
internal model. This model
gets input from other sensory
channels. If you open your
eyes after adapting to con-
stant-velocity rotation with
eyes closed, then the visual
signal accesses the vestibular
circuits, and the sensation of
rotation returns with a jolt
12
.
Although previous work had
demonstrated internal pro-
cessing and integration of
visual and vestibular sensory
signals, these computations
could be modeled by simple
circuits. In contrast, the dis-
ambiguation of gravitational
from inertial forces demon-
strates the sophistication of
vestibular processing and rec-
ommends the vestibular system as a
model for understanding how raw sen-
sory data are transformed to support
perception.
movement is consistent with a response
to an (illusory) head translation. Thus,
much as the ventriloquist manipulates
visual input to generate an auditory illu-
sion, Merfeld and colleagues manipulate
the vestibular canal signal to generate an
illusion of translation.
These two sets of experiments have
several important implications. First, eye
movement responses to rotation and
translation of the head are not mediated
by two distinct systems, but instead by a
single integrated system
8
. Second, otolith
signals are not interpreted as reflecting
tilt or translation based on a simple
method such as a frequency filter. Instead,
canal signals are combined with otolith
signals to produce a consistent measure
of head orientation and movement. Mer-
feld and colleagues argue that such a cir-
cuit should be considered an internal
model. It is a good bet that this circuitry
lies at least in part within the oldest part
of the cerebellum, the vestibulocerebel-
lum, portions of which have long been
implicated in vestibulo-ocular reflex
adaptation and, more recently, in the
extraction of rotational information from

V+Ves effect delay
The delay is undetectable when visual stimulus magnitude is near vestibular thresholds, and the delay vanishes in the presence of confirming vestibular cues of sufficient magnitude
* zvísi na integraci / boji V a Ves
http://www.mbfys.ru.nl/staff/j.vangisbe ... d_1988.pdf
Merfeld and colleagues rotate an
upright subject in the dark until the canals
completely adapt and the sensation of
rotation is abolished (
Fig. 3a
and
d
). This
happens because the canals are bony cir-
cular tubes, filled with fluid and spanned
by a flexible membrane (the cupola),
which behave somewhat like a bucket of
water. If you pick up a bucket and twist it,
the fluid at first stays still, and the bucket
turns around it. Friction of the fluid on
the moving walls of the bucket eventually
causes the fluid to ‘catch up’ to the buck-
et. In the canals, the initial lag causes the
fluid to exert force on the cupula, which
stretches in response. Hair cells register
this stretch, which modulates neuronal
firing. As the fluid catches up with the
canal, the elasticity of the cupula restores
it to its resting state, the hair cells no
longer sense stretch, and neuronal mod-
ulation ceases. This process takes about
twenty seconds, but the central ‘memory’
of the stimulus lasts longer, so the authors
wait two minutes for the rotating subject
Fig. 1.
Anatomy of the vestibular system. The
vestibuluar appartatus consists of three semi-
circular canals, which detect angular motion,
and two otolith organs (red and green), which
detect linear motion. The entire structure,
along with the cochlea, is encased within solid
bone in the inner ear.
Acceleration
Inertial
force
Gravity
Fig. 2.
Gravitational and inertial forces have
identical effects on the otolith organs.
(a)
A
hair cell from the saccule, stimulated by the
effect of gravity on the otolithic mass when
the head is tilted nose-up.
(b)
Same hair cell
stimulated by inertial force when the upright
head is accelerated forward. The hair cell
deflections in
(a)
and
(b)
are indistinguishable.
to lose all sensation of move-
ment. The subject is then
decelerated to a sudden stop,
which causes hair cells to sense
the cupula being stretched in
the opposite direction. Because
the canals and central circuits
were completely adapted to
(for example) a counter-clock-
wise rotation, this deceleration
produces exactly the same
response as an acceleration in
the opposite (clockwise) direc-
tion (
Fig. 3b
and
e
). Finally,
the subject is tilted nose-up
(
Fig. 3c
), and the eye move-
ments elicited by the vestibu-
lo-ocular reflex are used to
determine how the vestibular
system’s internal model inter-
prets this confusing input.
The vestibular system is
confronted with a paradox
(
Fig. 3f
). From the nose-up
position, the sensation of
clockwise rotation leads it to
expect the head to move so
that the right ear is down.
However, because no rotation
is actually occurring, the head
remains nose-up. The otolith
organs report that the back of
the head, not the right ear, is
‘down’. Hence the paradox: the
canals report that the head is rotating
clockwise and should therefore be turned
right ear down, while the otoliths report
a gravitational vector aligned with the
back of the head, as if no rotation has
occurred. To resolve this paradox, the
vestibular system postulates a leftward
force that would satisfy these conflicting
constraints. An illusory leftward inertial
force of the correct magnitude exactly
accounts for the difference between what
the otoliths report—that the back of the
head is pointing down—and what the
illusory rotation implies—that the right
ear is pointing down (
Fig. 3f
). Such a
force would be produced if the head were
accelerating to the right.
Subjects do not report translation, per-
haps because they are too disoriented by
the unusual sequence of stimuli to prop-
erly sort out their sensations. However,
their eyes betray them. Merfeld and col-
leagues compare evoked movements when
clockwise or counterclockwise rotation
precedes a particular head tilt. After sub-
tracting out the reflexive response to the
illusory rotation and the subsequent tilt,
a residual signal remains. This residual eye
otolith signals
9,10
. On the cur-
rent evidence, however, it is
not possible to rule out
involvement of the vestibular
nucleus.
The vestibulo-ocular sys-
tem has already provided sev-
eral less-complicated examples
of internal models. The cen-
tral ‘velocity storage’ mecha-
nism that maintains the sense
of rotation for a minute or
more after the canals have
adapted
11
is itself a simple
internal model. This model
gets input from other sensory
channels. If you open your
eyes after adapting to con-
stant-velocity rotation with
eyes closed, then the visual
signal accesses the vestibular
circuits, and the sensation of
rotation returns with a jolt
12
.
Although previous work had
demonstrated internal pro-
cessing and integration of
visual and vestibular sensory
signals, these computations
could be modeled by simple
circuits. In contrast, the dis-
ambiguation of gravitational
from inertial forces demon-
strates the sophistication of
vestibular processing and rec-
ommends the vestibular system as a
model for understanding how raw sen-
sory data are transformed to support
perception.
movement is consistent with a response
to an (illusory) head translation. Thus,
much as the ventriloquist manipulates
visual input to generate an auditory illu-
sion, Merfeld and colleagues manipulate
the vestibular canal signal to generate an
illusion of translation.
These two sets of experiments have
several important implications. First, eye
movement responses to rotation and
translation of the head are not mediated
by two distinct systems, but instead by a
single integrated system
8
. Second, otolith
signals are not interpreted as reflecting
tilt or translation based on a simple
method such as a frequency filter. Instead,
canal signals are combined with otolith
signals to produce a consistent measure
of head orientation and movement. Mer-
feld and colleagues argue that such a cir-
cuit should be considered an internal
model. It is a good bet that this circuitry
lies at least in part within the oldest part
of the cerebellum, the vestibulocerebel-
lum, portions of which have long been
implicated in vestibulo-ocular reflex
adaptation and, more recently, in the
extraction of rotational information from

Help! I'm a multidimensional being trapped in a linear time-space continuum!
Re: poznamky 2 - nečíst
Eye movement coordination: the vestibular-occular reflex
The vestibular-occular reflex is involved in the stabilization of eye movements during natural movement of the head when a person walks, runs or is exposed to vibration. The vestibular system exercises control over the eye muscles to stabilize an image of an object on the retina as the head moves. If the eyes moved directly with the head, the image of an object fixed in space would be degraded. The vestibular-occular reflex has an angular velocity approximately equal to but in the opposite direction of the movement of the head, which helps to stabilize the image on the retina.
When angular movement of the head is prolonged, the vestibular nystagmus is generated. The eyes, after their initial compensatory movements, quickly flicker in the direction of the turn and then start compensatory movements.
The vestibular-occular reflex is involved in the stabilization of eye movements during natural movement of the head when a person walks, runs or is exposed to vibration. The vestibular system exercises control over the eye muscles to stabilize an image of an object on the retina as the head moves. If the eyes moved directly with the head, the image of an object fixed in space would be degraded. The vestibular-occular reflex has an angular velocity approximately equal to but in the opposite direction of the movement of the head, which helps to stabilize the image on the retina.
When angular movement of the head is prolonged, the vestibular nystagmus is generated. The eyes, after their initial compensatory movements, quickly flicker in the direction of the turn and then start compensatory movements.
Help! I'm a multidimensional being trapped in a linear time-space continuum!
Re: poznamky 2 - nečíst
Posture and balance
The vestibulospinal reflex allows input from the vestibular organs to be used for posture and stability in a gravity environment. The projections from the vestibular system travel to muscles for coordinated movements that help to maintain posture. Changes in linear acceleration, angular acceleration and gravity are detected by the vestibular system and the proprioceptive receptors and then compared with visual information. A major role of the saccule and utricle is to keep the body vertically oriented with respect to gravity. If the head and body start to tilt, the vestibular system will automatically compensate with the correct postural adjustments (e.g., head-righting reflex).
Postural stability is maintained through vestibular reflexes acting on the neck and limbs. The vestibular apparatus signals the angular movement and attitude of the head with respect to the gravitational vertical. These reflexes are key to successful motion synchronization.
The vestibulospinal reflex allows input from the vestibular organs to be used for posture and stability in a gravity environment. The projections from the vestibular system travel to muscles for coordinated movements that help to maintain posture. Changes in linear acceleration, angular acceleration and gravity are detected by the vestibular system and the proprioceptive receptors and then compared with visual information. A major role of the saccule and utricle is to keep the body vertically oriented with respect to gravity. If the head and body start to tilt, the vestibular system will automatically compensate with the correct postural adjustments (e.g., head-righting reflex).
Postural stability is maintained through vestibular reflexes acting on the neck and limbs. The vestibular apparatus signals the angular movement and attitude of the head with respect to the gravitational vertical. These reflexes are key to successful motion synchronization.
Help! I'm a multidimensional being trapped in a linear time-space continuum!
Re: poznamky 2 - nečíst
Vestibular perception
The vestibular system has a relatively small cortical representation. Responses usually only intrude on consciousness, in the form of confusion, dizziness, and nausea, when they conflict with visual information during unnatural movements of the body.
Vestibular responses support several perceptual illusions:
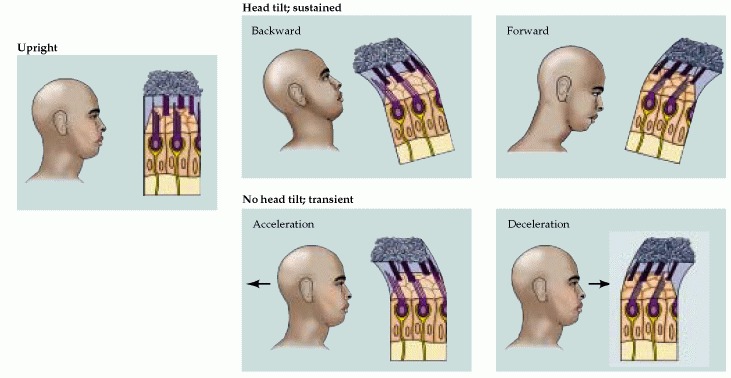
The oculogyral illusion—when an angular rotation of the body is stopped, illusory movement of the body and stationary objects occurs. Due to inertia, the fluid in the semicircular canals decelerates more slowly than the canals themselves. The resulting shear is in the opposite direction to that produced by the original rotation. (See Research study: see Research study: Magnitude estimates of the oculogyral illusion during and following angular acceleration: Parsons (1970).)
The oculogravic illusion—when the body undergoes linear acceleration, an illusory impression of body tilt occurs, because the otolith organs respond to linear acceleration and static head tilt without distinction between the two. Cohen (1973; see FP p. 73) reports that oculogravic illusions from forward acceleration are sufficiently powerful to elevate the visual perception of eye level.
Vection—when the visual surroundings are moved, illusory movement of the body occurs, either in the form of a translation (linearvection), or a rotation (circularvection).
The Coriolis effect—when the head is moved during an angular rotation of the body, illusory head tilt occurs as a consequence of the complex interaction of forces acting on the vestibular organs. Dichgans and Brandt (1973; see FP p. 74) report Coriolis effects even from apparent angular rotations of the body induced by circularvection.
The vestibular system has a relatively small cortical representation. Responses usually only intrude on consciousness, in the form of confusion, dizziness, and nausea, when they conflict with visual information during unnatural movements of the body.
Vestibular responses support several perceptual illusions:
The oculogyral illusion—when an angular rotation of the body is stopped, illusory movement of the body and stationary objects occurs. Due to inertia, the fluid in the semicircular canals decelerates more slowly than the canals themselves. The resulting shear is in the opposite direction to that produced by the original rotation. (See Research study: see Research study: Magnitude estimates of the oculogyral illusion during and following angular acceleration: Parsons (1970).)
The oculogravic illusion—when the body undergoes linear acceleration, an illusory impression of body tilt occurs, because the otolith organs respond to linear acceleration and static head tilt without distinction between the two. Cohen (1973; see FP p. 73) reports that oculogravic illusions from forward acceleration are sufficiently powerful to elevate the visual perception of eye level.
Vection—when the visual surroundings are moved, illusory movement of the body occurs, either in the form of a translation (linearvection), or a rotation (circularvection).
The Coriolis effect—when the head is moved during an angular rotation of the body, illusory head tilt occurs as a consequence of the complex interaction of forces acting on the vestibular organs. Dichgans and Brandt (1973; see FP p. 74) report Coriolis effects even from apparent angular rotations of the body induced by circularvection.
Help! I'm a multidimensional being trapped in a linear time-space continuum!
Re: poznamky vestibularni system - nečíst
Help! I'm a multidimensional being trapped in a linear time-space continuum!
Re: poznamky vestibularni system - nečíst

V > Ves(Ac)




Help! I'm a multidimensional being trapped in a linear time-space continuum!
Re: poznamky vestibularni system - nečíst
Ves = vestibular
G = gravitace
L = linerání zrychlení
W = angulární zrychlení (otáčení)

W

G = gravitace
L = linerání zrychlení
W = angulární zrychlení (otáčení)

W

Help! I'm a multidimensional being trapped in a linear time-space continuum!
Re: poznamky vestibularni system - nečíst
V leže na zádech
Konstrukčni bod 1 - Prostředek hlavy
osy
x - pravo , levo
y -dopredu,dozadu (nohy,hlava)
z - nahoru , dolu (oči,zadni čast hlavy)
Base sensory
V = tma
T = dotek z podložkou (+přikrývka)
W(x,y,z) = 0
L (x,y,z) = 0
G = 1g (z ,down)
p=0
L(y)
Akclerace směr před nohy nebo za hlavu
V = tma
T = dotek z podložkou (+přikrývka)
W(x,y,z) = 0
L (x,z) = 0
NL(y) not 0
G = 1g (z ,down)
L(x)
Akcelerace do stran
V = tma
T = dotek z podložkou (+přikrývka)
W(x,y,z) = 0
L (x,z) = 0
NL(x) not 0
G = 1g (z ,down)
L(z)
Akcelarace nahoru a dolu
V = tma
T = dotek z podložkou (+přikrývka)
W(x,y,z) = 0
L (x,z) = 0
NL(z) not 0
G = 1g (z ,down)
NL(z) +(up)
Zrychlování směrem nahoru
G(z)+L(z) vímanej nárust váhy , zatlačení do postele
Vizualizace - start rakety
G OK
T OK zvyšuje se podle L(z)+
P OK
V OK
*Raketa ve vesmíru G=O vnímáme pouze V(z)+ jako graviataci. Pri V(z)=+1g citime to sami jako pri G=1g a nemame jak rozlišit

*Výtah- priliš malá zěmna by to stálo za vizualizaci a zrychleni jen při startua zastavení

*Skok z letadla (odpor vzduchu)
*skok na černou díru (neni atmosféra)

Konstrukčni bod 1 - Prostředek hlavy
osy
x - pravo , levo
y -dopredu,dozadu (nohy,hlava)
z - nahoru , dolu (oči,zadni čast hlavy)
Base sensory
V = tma
T = dotek z podložkou (+přikrývka)
W(x,y,z) = 0
L (x,y,z) = 0
G = 1g (z ,down)
p=0
L(y)
Akclerace směr před nohy nebo za hlavu
V = tma
T = dotek z podložkou (+přikrývka)
W(x,y,z) = 0
L (x,z) = 0
NL(y) not 0
G = 1g (z ,down)
L(x)
Akcelerace do stran
V = tma
T = dotek z podložkou (+přikrývka)
W(x,y,z) = 0
L (x,z) = 0
NL(x) not 0
G = 1g (z ,down)
L(z)
Akcelarace nahoru a dolu
V = tma
T = dotek z podložkou (+přikrývka)
W(x,y,z) = 0
L (x,z) = 0
NL(z) not 0
G = 1g (z ,down)
NL(z) +(up)
Zrychlování směrem nahoru
G(z)+L(z) vímanej nárust váhy , zatlačení do postele
Vizualizace - start rakety
G OK
T OK zvyšuje se podle L(z)+
P OK
V OK
*Raketa ve vesmíru G=O vnímáme pouze V(z)+ jako graviataci. Pri V(z)=+1g citime to sami jako pri G=1g a nemame jak rozlišit

*Výtah- priliš malá zěmna by to stálo za vizualizaci a zrychleni jen při startua zastavení

*Skok z letadla (odpor vzduchu)
*skok na černou díru (neni atmosféra)

Help! I'm a multidimensional being trapped in a linear time-space continuum!
Re: poznamky vestibularni system - nečíst

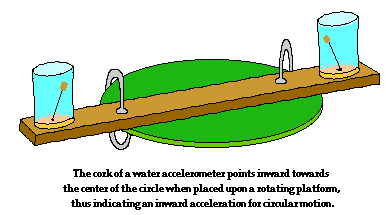
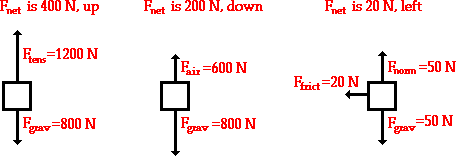
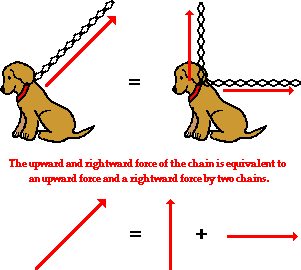
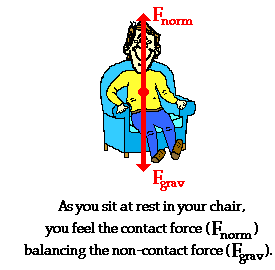
síla působící na tělo je v opačném směru než je směr akcelerace a rovná se F= m*g ale pusobý pouze jsme li v kontaktu z podložkou/stěnou..
Pohyb a vnímaný pohyb je ve směru akcelerace
Base
F(Gravity)= g(earth) * m(body)
Duležitě nevnímáme jen samotné zrychlení jako pohyb ale také jako sílu v opačném směru pusobýcí na části.Vnímání jak se přesune krev ve směru F.



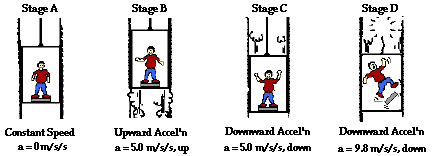
Help! I'm a multidimensional being trapped in a linear time-space continuum!
Re: poznamky vestibularni system - nečíst
base P G= 2,96
base P Ac=3,9
base P Ac=3,9
Help! I'm a multidimensional being trapped in a linear time-space continuum!
Zpět na „Lucid Dreaming Project“
Kdo je online
Uživatelé prohlížející si toto fórum: Žádní registrovaní uživatelé a 1 host